Pyramidal neurons represent the majority of excitatory neurons in the neocortex. Each pyramidal neuron receives input from thousands of excitatory synapses that are segregated onto dendritic branches. The dendrites themselves are segregated into apical, basal, and proximal integration zones, which have different properties. It is a mystery how pyramidal neurons integrate the input from thousands of synapses, what role the different dendrites play in this integration, and what kind of network behavior this enables in cortical tissue.
...
First we show that a neuron with several thousand synapses segregated on active dendrites can recognize hundreds of independent patterns of cellular activity even in the presence of large amounts of noise and pattern variation.
...
We then propose a neuron model where patterns detected on proximal dendrites lead to action potentials
...
We then present a network model based on neurons with these properties that learns time-based sequences.
...
We conclude that pyramidal neurons with thousands of synapses, active dendrites, and multiple integration zones create a robust and powerful sequence memory.
...
[Hawkins, emphasis added]
The quote above provides a convenient summary overview of the current state of understanding of the neuron. Addressed is one of the most important issues in the development of a broad understanding of the nature of neural function; why do neurons have so many synapses? The most common suggestion is that synapses must have a role in pattern recognition, learning and memory. But yet, all three functions are known to be information processing functions, which places them within the domain of computation. Little mention is made about how neurons with their complex dendrite trees and synapses might be able to support general computation. Any system which is capable of general computation must support the fundamental mechanisms required by general computation. But yet, the mechanisms by which neurons might be able to support computation are almost entirely absent from the literature on neural function, as it is in the publication quoted above. At the same time it is broadly accepted that the function of natural neural networks is fundamentally equivalent to computation; by the Church-Turing thesis all forms of computation are formally equivalent and therefore any function computed by a natural neural network may be computed by a Turing machine or it may be computed by a conventional digital computer, which uses a Von Neumann architecture. What the architecture of the various systems which support general computation show is that the underlying functional units of computation are very simple; they do not approach the complexity involved in processes such as pattern recognition, learning or any of the functionality generally attributed to neural networks. Instead, what is essential to computation is the ability to represent numbers and to systematically perform arithmetical operations on them.
At its most basic, a system capable of general computation must support three basic operators; the ability to increment a number, to decrement a number, and it must have a conditional repetition operation. These three operations form not just the basis of computation as we ourselves have developed it over the past century, but of any possible numerical system, no matter how different it might be. In contrast to the complex abilities often ascribed to the neuron, this minimal set of operations required to support general computation is very simple. Indeed, they are the simplest of all possible arithmetic operations on numbers. As will be shown, individual neurons are incapable of supporting any of these three operations, in the same sense that an individual transistor or an individual logic gate is equally incapable of supporting any of the fundamentals of computation. These fundamental operations, therefore, cannot take place within the cell body of an individual neuron. This contradicts the commonly held assumption that neurons are capable of high level functionality, and suggests that the current state of understanding of the neuron is fundamentally in error. Even fundamentals such as memory (the ability to store numerical values) are not supported either by the individual logic gate or the individual neuron. The theory of computation suggests that the operations which neurons support must in the first instance be those which support the ability to systematically store numbers and the ability to perform basic arithmetic them. Basic arithmetic allows for calculation; and it is the addition of conditional repetition to the basic arithmetic operations that differentiates the ability to calculate from the ability to compute.
At the most fundamental level, neurons are the atomic units of the nervous systems of natural organisms. This is what is asserted by the neuron doctrine, and has its origin with of Santiago Ramón y Cajal. The nervous system is, therefore, quite different from other elements of anatomy such as the vascular system, in which individual cells in effect merge to form a general circulatory system. With the nervous system, individual neurons link to other neurons but they function independently. In its simplest implementation, the nervous systems of a natural organisms can be seen simply as a mechanism for mediating the information produced by sensors and which is then received by the motor output. Sensors and motor outputs are themselves special types of neurons and all neuronal activity that is not produced by these two categories of input and output can be classified as intermediary (a product of inter-neurons). Some intermediary neurons have multiple inputs and all of the available inputs are integrated to produce a single output. While there is no strict upper limit to the number of inputs, the inputs are fundamentally dividided into two (and only two) categories; excitatory input and inhibitory input. Most of the neurons found in natural organisms are pyramidal in shape (and therefore often referred to as pyramidal neurons) and this leads to a natural representation of a neuron as a triangle; with the base of the triangle divided into two regions for the two types of input and the tip of the triangle representing its unitary output. The interior of the triangle represents the integrating function of the neuron.
The current understanding of neurons ends with the mystery of how neurons integrate multiple inputs, which can be excitatory or inhibitory. But yet, it is almost universally claimed that neurons are capable of pattern recognition, that they can learn and that they can store information. These claims are fundamentally misguided, almost self-evidently wrong and predicated on a fundamental misunderstanding of neural function. It may certainly be observed that neural systems as a whole are capable of recognizing or detecting patterns, capable of storing information and able to store information. It does not follow from these general observations that individual neurons have these abilities. Neural systems are certainly able to recognize grandmothers but it is almost self-evidently wrong that an individual neuron would have the ability to do this. By the same reasoning, if the control software of a self-driving automobile is able to detect a grandmother and is able to effectively navigate so as not to bring any harm to her, then that recognition function must be resident within a single logic gate (which is the atomic unit of that system). Because we understand how this control system functions (because we designed and built it ourselves) this hypothesis would be self-evidently absurd. We know that the algorithms which are responsible for the recognition are several layers of abstraction removed from the actual hardware that is used to implement the system and that any one of the billions of hardware units of that system have at best a fleeting and arbitrary relation to those algorithms. It would be self-evidently absured to take the view that the algorithm was somehow physically resident in one of those units.
The current approach to the funtion of neurons is therefore inherently contradictory. The contradiction is between the fact that we know that neural function must be simple and the need to explain the complex functionality of neural systems with neural function. We currently understand that all computation, no matter how complex, can be expressed in terms of three simple operations. In almost a century of research, there has been no evidence to contradict the universality of computation. Some of the functionality of the neural systems of natural organisms is currently understood in terms of conventional computation. The information processing for audition, for example, can be understood in terms of wave theory and fourier transforms, which can readily be implemented using conventional computation. Yet some of the functionality of natural organisms seems intractable. This failure to understand naturally leads to the desire to attribute those abilities to an outside agency (such as an oracle). This explains the need to place the ill-understood activity of neural system within the neuron itself, making the ability essentially unknowable. But yet it is known that this ability, no matter how intractable it appears, must be expressible in the simple terms of computation. While it may be the case that neurons incorporate complex functionality, there is little to be gained by focusing on these complexities when the simple and essential functionality is as yet not understood.
How neural systems function is currently a mystery, and not at all understood. When something is poorly understood humans are prone to ascribing it to an outside agency, sometimes for clarity and convenience referred to as a deiety. In the realm of information and processing this is by convention referred to as an oracle. The claims that individual neurons have fantastical abilities which are self-evidently not only untrue but could not possibly be true all treat neurons or neural systems as if they were oracles. A neuron that recognizes a grandmother or a neuron which learns or a neuron which remembers is essentially an oracle. Oracles do not need to be fantastical. A hard disk is device which allows an essentially unlimited amount of information to be stored and recalled and is therefore from the point of view of computation in effect an oracle. Quantum calculation may be considered another type of oracle, although it is not yet clear whether this can in practice be implemented. Oracles are therefore useful as a kind of placeholder for specialist functionality which lies outside the bounds of conventional computation. It would be extremely unhelpful to invoke oracles when developping an understanding of the core functions of a system of computation. Oracles should therefore have no real place in developping an understanding of what neural function really is. Unlike our ancestors, we do not wish to celebrate or worship the oracle, but rather we insist on understanding the oracle so that we can design and build it ourselves. In fact we have no need for oracles to help us understand neural systems because we already understand what it is that neural systems do.
By the Church-Turing thesis we can be reasonably certain that the activity of any natural neural system is formally equivalent to computation, and within that domain it may be proven that anything equivalent to computatation is itself compuation. A century of the study of neural systems has left little doubt that neural systems are computational systems. They are not oracles, in the sense that they are capable of producing answers that are outside the bounds of computation as we currently understand it to be. This has led to the view of neural systems as computational systems to be broadly accepted. This is, however, at odds with the intractability of the problems that neural systems seem to be able to solve (such as recognizing grandmothers). This provides the motivation for invoking the oracles of learning, detecting, memorizing and so forth. What these oracle-like abilities of learning to recognize your grandmother by remembering what she looks like have in common is the ability to change. Yet, we know with mathematical certainty that the fundamental units of computation cannot and must not change. Therefore, the individual neuron cannot have oracle-like abilities such as memory, recognition and learning.
Why is it that the neuron is so ill-understood? Principally, it is because of neural complexity and a lack of understanding of the principles of computation and the nature of information by those who study neural function. A subtle implication of computation is multiple layers of abstraction, and this leads to a great deal of disassociation between function and the hardware which implements the function. These layers of abstraction are almost impossible (for us) to reverse engineer, even if we ourselves designed the system. This complexity must be contrasted with the underlying simplicity of computation. It is those underlying principles which should be the focus in respect of developping an understanding of neural function. It is this function that neurons must be able to support directly.
What are the fundamentals of neural systems that underpin computation. The first thing that any system of computation must suppport is the ability to represent numbers. If we greatly simplify neural systems what we are left with are simple feed forward systems which translate sensor values to action potential sequences and those action potential sequences travel through the system and drive some form of motor function. This can readily be understood as analog to digital conversion at the sensor stage and then conversely digital to analog at the motor stage. This clearly demonstrates that neural function is numerical in nature, and it shows that the fundamental role of a neuron is simple repetion. The neural code exists primarily to allow sensor values to be transmitted over long distances without any loss of information. The action potential of a neuron is an all or nothing event but the code is not necessarily digital. A digital code is what is used almost universally in the systems capable of computation that we ourselves design (to do things like autonomous driving). That means the numbers are inherently integers, with the degree of precision as part of the design (8-bit, 16-bit, 32-bit etc). Digital system could use an action potential code using time division to represent each binary digit. However, neural systems do not use such a code. Neural system use the distance between action potentials to code a sensor value or to determine the degree to which a motor function is activated. This is inherently an analog measure. This suggests that neural systems are based on real numbers, rather than the integer numbers that digital systems are restricted to. This has a very important consequence, which is that precision can be arbitrarily increased without having to redesign the entire system. Moreover, practical digital systems have demonstrated the need for real numbers by the development of floating point arithmetic, which is a digital implementation of real numbers.
Numbers are fundamental to any system capable of general computation. Turing machines traditionally use unary to code numbers, Von Neumann machines are best suited for binary numbers, and it appears that natural evolution has opted for real numbers for neural systems. This has benefits, but it also has drawbacks. Computation requires not only numbers, but operations on numbers. Any calculation can be done by just two simple operations; increment and decrement. It is therefore not a coincidence that neurons have two basic inputs; excitatory and inhibitory. If the basic function of a neuron is taken as simple repetion, then a restricted case of excitation and inhibition is repetition with the ability to increase or decrease the value that is repeated. This is equivalent to the ability to increment and decrement, but with an important limitation due to numbers being represented without a discreet limit.
The next step from the ability to increment and decrement numbers is general arithmetic – addition, subtraction, multiplication and division. Excitation and inhibition inherently equivalent to addition and subtraction. Multiplication is equivalent to repeated addition and so would is straight forward to implement in the simplest cases. While division can also be implemented by repeated subtraction this is not symmetric with multiplication. With multiplication the simplest multiplication (×2, ×3, ×5 etc) is the easiest, whereas with division the simplest division is the most difficult. In fact in the simplest case, which is simply dividing my 2 or 3, this involves so much repetition that it would not be practical. Furthermore, a number can be doubled or tripled by the simple expedient of duplication which is inherently an integer function. A number can be duplicated with itself, but there is no natural inverse of duplication. Any natural neural system no matter how simple would have the need for simple arithmetic. Addition, subtraction and simple multiplication can be achieved by very simple neural circuits. Simple division cannot be achieved in the same way. Since all complex neural systems have developed from simple neural systems all neural systems have had the need to develop a form of simple division. This is the key to understanding neural complexity. The central mystery of neural integration can be solved by seeing it as simply a limited implementation of basic arithmetic. Why do neurons have thousands or tens of thousands of synapses? It is not to learn or to store information, but rather it is because of a need for precision. A neuron with more synapses is able to divide a real number more precisely into components, and thereby is able to achieve greater precision. In terms of digital computation, if we say that some neurons have a dendritic tree of 256 , 1024, 16384 or 65536 branches then the purpose of the dendritic branching might be more apparent. We could summarize these more simply by stating the bits of precision, and we can see that neurons are capable of 16 bits of precision, with perhaps up to 18 bits in extreme cases. (with neurons such as the Purkinje ne)
There has been considerably excitement in recent decades about ‘neural networks’[Crick]. Yet, despite three decades of feverish activity and increasing ‘excitement’ no neural network has yet been shown to be capable of carrying out useful computational tasks. Demonstrations of useful activity have been at best misguided and at worst fraudulent [link to Deep Mind]. The nature of the activity inherently stems from a fundamental misunderstanding of the role of a neuron within the brains of living organisms. Neurons do not inherently ‘learn’, recognize patterns (such as ‘grandmothers’) or remember. Learning and pattern recognition are naturally activities that the simplest of natural organisms seem to be capable of, while at the same time those function have proven to be very intractable with respect to digital computation. It is therefore often assumed that the fundamental unit of neural systems must be capable of these functions, which are inherently missing from the fundamental units of digital computation.
It is often the case that the first step toward solving a problem is framing the nature of the problem correctly. Sometimes problems are deceptive and take advantage of inherent human weaknesses. One such weakness is to dive into the detail without first looking at the depth. Its usually unwise to dive before checking depth. In fact, some problems can be infinitely deep (like fractals). Usually when investigating something we want to get to the ‘bottom’ of things, which is where we establish the foundations for a theory and then we build upwards from there. This is a good idea in most cases, but one should not assume that this what you should do in all cases. Assumptions can sometimes make you look like an ass at the most inconvenient of times. Looking like an ass can of course have dire consequences, so most researchers will go to considerable lengths to avoid this fate – and this leads to another weakness, the tendency to make things so complicated that no one else can understand it and thereby making whatever is being proposed immune to criticism. Usually these unfortunate tendencies are to some degree self-correcting, especially with knowledge of principles such as Occams razor that derive from a long history of unnecessary complexity.
One need only look at the vast amount of literature that exists on the subject of the neuron to see that the neuron may be said to be purposefully designed to take maximum advantage of human weakness for ornate complexity. From a distance is appears to carry out a simple function, but as we examine it in greater detail we find inordinate and impenetrable complexity. A single neuron for example may have a dendrite tree of about 100,000 branches. Surely a neuron with a dendritic tree of that complexity must do something important and complicated, and by extension someone must work out what that important and complex function might be. So what exactly is it that neurons actually do? Neurons connect with other neurons into vast networks, and those networks of neurons do things which we have trouble understanding. Things like learning, storing information and recognizing grandmothers. Perhaps it makes some kind of sense to think that what the neuron with a dedrite tree of 100,000 nodes is doing is recognizing grandmothers or storing information.
While grand-mother detecting neurons might seem like the concluding statment of a reductio ad absurdum argument, it is actually the current level of understanding of neural function. For those who do not see that the claim of a grand-mother detecting neuron is self-evidently absurd it might be useful to approach the subject by analogy. Not only is it suggested that neurons can ‘detect’ grandmothers, but they an also ‘learn’ to detect grandmothers.
So what is it that neurons do? What is its most basic underlying fundamental function, in the simplest case? To answer this one has to pay attention to the evolutionary history of neurons, to the extreme distant past which saw the origins of multi-cellular organisms. Many organisms survive without any ability to actively sense the environment or to adapt their behaviour to the environment. Those that do have the ability to sense the external environment started with the simplest of sensors and respective motor controls. The simplest case of sensor-motor control is when a sensor connects to and drives a motor directly without any intermediary circuitry. These distant sensors were much simpler than conventional neurons, in that they merely produce an electrical potential in response to the degree to which they are stimulated. They do not ‘fire’ or produce any complex activity. We know that sensors worked in this way in the very distant past because these sensors have remained largely unchanged since their origins in that distant past. They continue to exist in us and in all the animals that currently exist, no matter how large or small. An ‘electrical synapse’ (or gap junction) transmits the actual state of the neuron and is therefore directly analagous to the sensors we ourselves use to measure various natural phenomena. The electrical potential may be seen simply as an analog value between a minimum and maximum, and the gap junction as a window through which that electrical potential may be transmitted or measured. In the simplest of organisms this junction links directly to the ‘motor’. This motor may be a simple flagellum which propels the organism or it may be a ‘muscle’ which contracts to perform some function. In any case, the value of the electrical potential drives the motor in proportion to the strength of the potential.
When an animal consists of just a few specialized cells then there is no obstacle to sensor neurons driving the motor output directly. As the animal grows larger then the neurons can for a time adapt by 'stretching'. Eventually, however, a limit will be reached as to how far a neuron can be elongated. It is possible for a signal to be passed through a few intermediate neurons, but electrical potentials degrade rapidly each time they are passed on, and there is as a result a natural limit to this approach. Elongation of the sensor neuron also in itself degrades the electrical potential significantly. Evolutionary pressure on an organism to become larger and larger therefore places an evolutionary premium on a general solution for long distance communication. The solution to this evolutionary need is communication by action potentials, which are electro-chemical spikes able to propagate rapidly and propagate over long distances; and importantly, which can be reproduced precisely without any loss, even with significant attenuation of the signal. The neuron and its underlying function therefore has its beginning as a simple propagator of an electrical signal; addressing the need to send a signal over longer distances, which in the simplest case, is simply from sensor to motor. There is no adaptation, no 'learning' and no ability to recognize ‘grandmothers’. The function is purely and simply repetition. Indeed any deviation from accurate repetition would be undesirable. The ‘chemical synapses’ that enables this long distance communication are much more complex than the simple physical junctions which essentially joins two cells together via an electrical link and this requires additional more complex functionality within the cellular mechanics of the individual neuron.
Although the electro-chemical spikes in potential are able to travel extended distances compared to a simple electrical potential, this distance is also limited. Longer distance communication requires insulation, and this is provided by another innovation – specialist cells which wrap around the extended process of the neuron which carries the spike-like action potential from the central region of the cell to the distant synapse.
Establishing the fact that the fundamental role of a neuron is simply repetition allows the foundations of a neural doctrine to be established. All intermediary neurons that transmit information from a sensor to a motor have their origin with repetition. In the simplest case the intermediary neurons merely bridge the gap between sensor and motor, with the action potential itself having no inherent meaning. That is established by the way that the analog electrical potential is tranlated to action potentials, and inversely how action potentials are translated back into an analog potential which is able to drive a motor. In the base-case of sensors driving motors directly and neurons being used simply to bridge the distance between sensor and motor, the simplest way to code electrical potential is by temporal distance between action potentials; the maximum potential is coded by a minimum distance between action potentials (which is the neuron's maximum firing rate), with the firing rate declining in inverse proportion to the electrical potential. How information is coded by the action potentials is therefore established by sensor/motor coding and decoding – what is in effect an analog to digital and digital to analog conversion process, with specialist neurons performing this function. While an action potential is inherently either on or off, the action potential itself does not represent information. Its role is simply that of a temporal marker for the information coding process. In the simplest case, where information is represented by the rate action potential are produced, it is the temporal distance between action potentials that is used to code information. This requires a minimum of two action potentials to evaluate the temporal distance between them, and it implies less latency for high values than for low values.
The electrical potential of a sensor neuron when it is transmitted via an electrical junction may be seen abstractly as a numerical value. A sensor may therefore in effect be represented as a continuous variable. These values are not discrete integers coded in binary but rather real numbers representing an arbitrary degree of precision. In the simplest case, of an animal where the sensor input only has to be transmitted to the motor output by means of intermediary neurons that fire action potentials the ‘code’ that these action potentials represent is very simply the distance between action potentials. The maximum firing rate represents the maximum sensor input and the minimum firing rate represents the zero condition when there is no sensor input. The firing rate is then translated back to an electrical potential at the motor, which is activated exactly the same way as it was previously with a direct electrical connection between sensor and motor.
Simply by looking at the distant evolutionary history of neurons when organisms were very simple therefore allows us to establish the fundamentals of neural communication, and solves one of the most vexing issues in current research on neurons and neural networks – what does an action potential represent? An action potential by itself has no meaning, and also the average number of action potentials over time has no meaning. In the simplest case, it is the temporal distance between action potentials which codes information, but it is the coding and decoding process that establishes this. When sensors drive the neural code, the information coded is continuously variable and therefore the distance between individual action potentials varies in line with the information coded at a specific instance in time. The two principles that neurons repeat action potentials and that action potentials code numerical information by the distance between action potentials is the foundation of a neural doctrine. This is of course an abstract model, which does not necessarily reflect the underlying principles of real-world neurons. It is undoubtedly the case that within the undiminishing complexity of real-world neurons a contradiction can be found to what is in effect a simplifying model. This should not be the measure of success or failure of the model, however. In the span of less than a century digital circuits have evolved to great complexity by the actions of our own hands, and this increasing complexity has led to a wide variety of specialist devices which are inconsistent with the overall digital paradigm. Their existence, however, does not break that overarching paradigm. Equally, in a billion years of evolution specialist neurons may well have developed which perform a wide variety of specialist functions. The test is not that the model explains all types of circuit irrespective of the specializations and shortcuts that have been developed over time, but rather that the underlying model can explain the underlying principles – and that is demonstrated by the fact that it works; that it is useful and can be used to produce the same functionality. And it is very important to pay attention to what that function is. It is most certainly not 'learning' and recognizing ‘grandmothers’. The problems are most certainly much more simple. How, for example, can we get an animal consisting of just a few hundred cell to swim in a straight line? How can this same animal circle slowly when in the sun but swim rapidly away from a looming shadow?
If we follow the needs of an idealized simple animal which functions by motors being driven directly by sensor input, it quickly becomes apparent that it would be of great benefit to that type of animal if its neurons were able to do more than simply repeat action potentials.Evolution is by nature a tinkerer [Crick], and once an underlying principle has been established, variation of that principle will invariably emerge. Motor activity which is directly driven by sensor input is useful and better than flying blind, but it is very limited. It it is certainly useful to have the ability to swim directly into the sun or toward the scent of food, but it may be even better to change the angle by a few degrees when approaching to avoid being lured into a trap. Simple changes to the neural code can achieve these kinds of small modifications easily. Such simple changes may be achieved by specialist neurons that, for example, decrease the action potential rate slightly in the way that they repeat action potentials that are received. Neurons that do not simply repeat action potentials but are able to modify the action potential streams (spike trains) are therefore very useful, and it is very useful for this ability to be generalized rather than having every function specifically defined in hardware. It may be useful for example to be able to slow the firing rate of a neuron in relation to a sensor input rather than simply hardcoding a fixed decrease that cannot be dynamically changed. This need to have the ability to modify action potential sequences dynamically naturally leads to a neuron that is capable of the simplest of such change – the ability to increase or decrease the action potential rate based on a third input. Neurons with this ability may be said to increment or decrement the action potential rate. While the fundmantal role of the neuron remains repetion of action potentials, they will also have excitatory and inhibitory inputs that can increase or decrease the rate at which action potentials are repeated. This ability may initially have a haphazard implementation but due to its importance may well over time be generalized. The generalization of increment and decrement leads to general arithmentic.
A system that simply repeats signals produced by sensors is by necessity a feed-forward system. All values originate outside of the system and all activity of the system is driven only in the forward direction toward the output.
What is required for the simplest of more complex behaviour is the ability to carry out basic arithmetic; to be able to add and subtract. It can readily be shown that addition and subtraction can easily be incorporated into a repeating neuron by a simple mechanism of increasing or decreasing the firing rate. The simplest implementation of addition is just to allow multiple inputs, where each action potential irrespective of input is simply repeated. This may be somewhat imprecise as the distance between outgoing action potentials will be variable and the output will only approximate addition. Also, some action potentials will be lost if action potentials overlap. Nevertheless, a crude intermediary solution will clearly over time lead to a proper integrating function which will produce correct summation function. Subtraction is more complex but an integration function capable of addition would by extension also be capable of subtraction. Subtraction is therefore requires the development of a 'subtractive' input; an inhibitory synapse.
Addition and subtraction are very useful and can be used to produce a wide variety of complex behaviour. Indeed, all calculation can be done with just addition and subtraction. This may well be the reason that neurons are capable of addition and subtraction (with synapses being either 'exciting' or 'inhibiting'). Nevertheless, with increasing complexity it is often convenient to have more mathematical operators, with multiplication and division being the most important. A neuron that is capable of integrating action potentials from multiple sources in a way that is consistent with addition is also capable of multiplication. Multiplication is simply a multiple of addition. Multiple inputs which repeat the same signal allow a neuron capable of addition to perform multiplication simply by adding more synapses. For example, a neuron with two inputs which receives the same input performs addition but in fact implements multiplication by 2. For a simple animal, the most common need would be for low order multiplication; ×2, ×3, ×4 and so forth. In this sense, multiplication is trivial to implement with this model of neuron. Division on the other hand is difficult to implement. Division can be described as repeated subtraction, but low order division (which is most needed) is the most difficult.
While a great deal of work has been devoted to understanding the physiology of neurons, comparatively little attention has been paid to neurons as fundamental units of computation (or indeed calculation). It is broadly accepted that what the brains of natural organisms do is computation. By the Church-Turing thesis all computation is equivalent, and it follows from this that the activity of any computional device can be emulated by any other computational device (as long as it is Turing-complete). This is of course a conjecture that has not been formally proven, but it is broadly accepted as true. Importantly, it has never been contradicted.
What then is the fundamental function of a neuron? The neuron is fundamentally a repeater. It is not an adder, a subtractor, a logic gate, a memory unit or a pattern recognition unit. Its job is a very simple one. It receives an action potential and it simply repeats that action potential with as little delay as possible.
It is common to think of a neuron as computing a single weighted sum of all of its synapses. This notion, sometimes called a “point neuron,” forms the basis of almost all artificial neural networks... [Harris]
It is difficult to imagine a construct more unsuited to supporting computation than a weighted sum. It almost seems purposefully constructed to obstruct any real understanding of neural function. The most basic fundamental role of a neuron is repetition, which in the simplest of neural networks is just repeating the values produced by sensors and directing them toward the motor function of the organism. Positing the neuron as as a unit that computes a weighted sum is analagous to placing a a low-pass filter over your eye in order to study vision – it simplifies the image but it means most of the visual information is lost. Computing a sum must in the neural domain of all-or-none action potentials be a temporal function. A neuron which performs a temporal sum cannot be a neuron that able to simply repeat action potentials. A sum is necessarily an averaging process over a specific temporal period and this means that a neuron will inherently be opaque to the information it receives at its synapses. The underlying principle of computation is that information must not be lost by the functional units which are used to perform the computation. Even if this type of fundamental unit of operation could be moulded into processing information in a way that is Turing complete this is unlikely to be practical and useful. Indeed, no artificial neural network has been shown that carries out any of the fundamental operations required by computation, and in fact even the calculation of basic arithmetic has been shown to be a challenge. Instead the aim for artificial neural networks has almost universally been to demonstrate their application to problems that appear intractable to conventional computation – problems such as recognition, pattern detection and learning. They are used as helper functions to conventional computation – essentially as an oracle that learns to recognize grandmothers. What is the first step that these grandmother detecting oracles perform? It is invariably doing a Gaussian blur, which removes most of the information. What kind of doctor would start a consultation by throwing away most of the information about the patient? Only one kind of doctor – the kind of doctor who has only one diagnosis and whose remedy is invariably the one type of snake oil that he happens to sell. Snake oil might initially appear to solve a problem, but ultimately it is invariably useless (or even worse than useless). In the same way, artificial neural networks are not neural networks at all; they do not and cannot support computation in any useful way and ultimately they detract from a genuine understanding of real neural networks.
While it is tempting to conclude from the empirical evidence about neurons that they integrate their input simply by temporal summation (with incomming action potentials increasing the neurons internal electrical potential until some arbitrary threshold is reached, at which point the neuron fires off an action potential of its own), this is not a model which easily supports the fundamental operations that support general computation. Indeed, the simplest form of a weighted sum – an weighted sum with all weights set to 1 – is unable to support the most simple basic form of neural communication, which is simply to repeat action potentials. The neural code represents information, and computation is only possible if the underlying units which support that computation are capable of preserving the information on which they act. A neuron that repeats action potentials preserves the information held by the neural code, but a neuron which performs a temporal sum does not. While the latter model appears simple, it also implies intractable complexity. A central threshold which determines when the neuron is sufficiently stimulated to fire an action potential requires a stored value representing that threshold. Furthermore, a weighted sum implies that each individual synapse also maintains a stored value. The fundamental units that support computation cannot support stored values because there is no way to systematically address or change the stored values. It is important to note that artificial neural networks, which almost universally use the weighted sum model, invariably use an outside (computational) agent to set these stored values, a process which is generally referred to as training the artificial neural network. Real neural networks have no external agent which is able to compute these stored values. Practical implementations of artificial neural networks have also found that large numbers of synapses are unecessary and counterproductive. The neurons of real neural networks may have up to several hundred thousand synapses, and this is an order of complexity that cannot be maintained without an underlying management framework. It should be noted that early computing systems were able to provide useful functionality with as little as 1024 stored values, with most of the architecture of those systems being dedicated to supporting mechanisms to access those stored values. The atomic units of conventional digital computation are logic gates, which on their own are incapable of storing information. The ability to store binary eight bit numbers requires networks of thousands of logic gates. It would be very unlikely that the atomic unit of neural systems is itself able to store information two orders of magnitude greater than entire systems of computation.
While the weighted sum model of neural function results in a loss of information and is fundamentally unsuited to simple communication, it is possible to modify the model to make it more useful. Rather than a central threshold, it is more useful to assume that the central integrating function of a neuron is simple repetition. A repeating neuron is equivalent to a threshold neuron where the threshold is set at a level equal to or less than the strength of a single action potential. This is consistent with neurons that have only a single excitatory input, and which simply repeat the neural code which they receive. Repetition can be implemented simply by repeating every action potential that is received, which avoids the complexities of integration. Any action potential received by a synapse will lead immediately (or with as little delay as possible) to the production of an action potential.
Repetition is very useful, even for complex neural systems. It allows sensory input to travel distances greater than the reach of a single neuron. Most neurons, however, have multiple inputs. Neurons with multiple inputs are know to have excitatory inputs and inhibitory inputs, and the synaptic input of these multiple inputs must be integrated to form a single action potential output. If this central function of the neuron is assumed to be addition (when the synaptic input is excitatory) and subtraction (when the input is inhibitory) then this greatly simplifies neural function. While integrating unsynchronized action potentials in a way that is consistent with addition is complex, it is simpler to assume that neurons function inherently in the same way as sensors; that they release action potentials not because of an internal threshold but rather that they produce action potential sequences in relation to their internal electrical potential. Any non-zero potential of the neuron will cause the neuron to fire action potentials at the rate proportional to the potential, and any non-zero value always begins with an action potential. This initial action potential is very important because the neural system as a whole must function with a minimum of latency. While simple repetition can be implemented directly so that receipt of an action potential drives the production of an individual action potential that is sent out with an absolute minimum of delay, this function can also be implemented more indirectly if the internal electrical potential of the neuron is determined by the temporal distance between incoming action potentials. In this way the action potentials that are received do not necessarily need to come from the same source. This may be seen as a type of summation but it does not rely on a threshold, and therefore does not require a stored value. It is consistent with the conventional weighted sum model in that action potentials that are received increase the neuron's electrical potential and this potential decays over time if no action potentials are received. The difference is that a neuron fires according the level of this potential rather than when that potential crosses some arbitrary threshold. Because each neuron represents information internally in the same way that sensors do, this means that the action potential code is translated back and forth at each neural step. The advantage of doing this is that the action potentials from multiple sources can be as easily integrated as if the synapses receiving the temporal all-or-none action potentials were continuous value electrical junctions.
Treating neurons as if they were a variant of sensor is consistent with their evolutionary history, where all the inter-neurons are preceeded by very simple neural systems that consist only of sensor and motor neurons. The earliest inter-neurons that connect a distant sensor and motor neuron to each other would be electrical junction neurons. With greater distances these electrical junctions would become impractical and this leads to the need for a solution to carrying the analog value of a sensor neuron to a motor neuron, which is also requires an analog value. Synapses and action potentials are the solution to that specific problem, and the earliest forms of synapses and action potentials were most certainly variations of electrical junctions that were over time became more refined. It is therefore reasonable to assume that a synapse is essentially a digital to analog converter; converting sequences of action potentials to an analog value, in the same way that external input (such as discrete photons) produces a sensor value. Indeed, a synapse may be seen as a variant of a sensor model. In the same way that receipt of a single photon is amplified, the receipt of an action potential is also amplified so that any action potential received, no matter how weak, is reconstituted to produce a constant analog value, which then propagates to the integrating center of the neuron. Integration is then simply summation of the values produced by the synapses on the dendritic tree, and a neuron will fire at the rate implied by the summation.
For neurons with thousands of synapses, if the strength of each synapse was equal then the quantity of its input would rapidly exceed its ability to produce action potentials. This is the reason why synapses are generally considered to have a weight, which reduces the synapses ability to stimulate the neuron. While an arbitrarily weight for each synapse is impractical and not generally useful for supporting general computation, empirical study of neurons supports the hypothesis that synaptic input is weighted. This weight is, however, not necessarily an inherent part of the synapse itself (present as a stored value) but rather it may simply be a function of distance and branching of the dendritic tree. If a synapse translates an incoming stream of action potentials into an electrical potential it is the dendrite which transports this potential to the integrating center of the neuron. Electrical potentials naturally decrease with distance, and therefore the further a synapse is from the integrating center the weaker the electrical potential. Distance on the dentritic tree is not really a reliable metric, but it is possible that early simpler neurons took this approach to moderating multiple inputs and that this approach was then formalized over time. While a dendritic tree appears chaotic, branching is in fact quite regular and well defined. Branching is always an integer component, with dyadic branches being the most common. If we assume that the weight of each branch is equal to the number of components of the branch, then this avoids the need for stored values. It would also have the very useful side-effect of integer division. A dyadic branch would divide by two, a triadic branch would divide by three and so forth. Because branches can be nested, higher order division can be performed very simply by increasing the nestedness of the branching. Each synapse is in effect converts a digital action potential code into an analog value and this value is reduced with each branch as it travels to the integrating center of the neuron.
If the purpose of branching is integer division then the reason for complex dendrite trees with thousands or even hundreds of thousands of branches becomes almost self-evident, especially if we assume that branching is mostly dyadic. A dyadic dendrite tree with 262,144 end nodes might appear unnecessarily complex, but it allows for only 18 bit division. This is essential for the degrees of precision that the system as a whole is capable of. Empirical evidence suggests that the limit of precision in humans is between 16-18 bits. The limit for auditory information is in this range and visual information is in the range of 10-12 bits. Motor control requires the greatest degree of precision and in humans it is known that the neurons with the greatest degree of branching are involved with the most precise motor control. Neural branching may therefore be seen as function of precision rather than as a store of information. Neurons that have hundreds of synapses, would be capable of 8 bits of precision; thousands of synapses would indicate 10 bits of precision and tens of thousands would indicate 16 bits of precision.
The reasons why neurons can only achieve precision with a high degree of dendrite branching is not immediately apparent from a neuron that simply needs to reduce the level of its inputs. But it becomes quite clear when the underlying needs of computation are taken into account. The fundamental operations of computation are increment and decrement. For digital systems which code only for binary coded integers this is trivial. However, for a system which codes real numbers using an analog method, numbers can only be incremented or decremented with reference to a known degree of precision. A numerical value itself has an arbitrary degree of precision. Increments and decrements can therefore only be fractions of a known value. Calculating these fractions can be considered a fundamental operation for this type of system, which in effect is an analog model of computation. As an example, consider an arm which has to hold a weight. The input to the motor has to be set precisely equal to the weight which must be supported. This requires a feedback system which adjusts the motor power in proportion to any variation. This adjustment would be in proportion to the current motor output. Assuming the motor output is never constant (due to inherent instability) then the degree to which a weight may be held in one constant position is proportional to the degrees of precision available. The position will appear stable, but the sensors will record constant variation which is then conteracted by the motor output being varied constantly by very small amounts to maintain stability. If the available precision is reduced then the degree of that that motion variation becomes apparent. This is exactly what happens in humans and other animals when the complex dendrite tree of the neurons that control movement are degraded. Movements becomes shaky, or jerky. For an analog system the way that numbers are processed is similar to the way measurements were performed under the old SAE system of measurements. Tools were not specified by an absolute measure, but rather by fractions of an inch. A tool might be a quarter of an inch, and if it did not fit one would try a half inch tool and if that was too big then more precision was needed and one would try 3/8'ths of an inch. The approach to measurements would be the same for neurons. A neuron might branch two times, producing four end nodes, and this would allow a neuron to connect to between one and four synapses. Connecting to the synapse of a single end node would represent 1/4 of the incoming rate. By connecting to the synapses of the other end nodes, 2/4, 3/4 and 4/4 of the input rate can be signalled. This would represent two bits of precision. If greater precision is needed then the dendritic tree can simply be increased. In this way dyadic trees can be used as a digital overlay onto an analog system.
This type of neuron, which has the ability to perform centralized addition and peripheral integer division, is very useful in supporting computation. Being able to divide unbounded real numbers by integer degrees is not only useful for functionality like high precision feedback applications but it is also essential for being able to implement the core functions which support general computation.
Traditional approaches to neural coding characterize the encoding of known stimuli in average neural responses. Organisms face nearly the opposite task – extracting information about an unknown time-dependent stimulus from short segments of a spike train. [Bialek]
The assumption that the information about the external world is in some way encoded in the action potential sequences of neurons is an error of reasoning. Organisms certainly are able to recognize and react to external stimuli, and this is most certainly a result of neural activity within the neural network of the organism. It does not follow that there must be information about the stimulus present in specific action potential sequences or in the activity of individual neurons. The error stems from the assumption that the external world consists of signals which the neural sensors are tuned to and which provide useful information about the external environment. By way of analogy, an electronic device such as a radio or television is tuned to the signals which contain the information the respective device is designed to receive, and the device's primary function is to decode this information. Natural organsims are not like radios or televisions. There is no information in the natural world to decode. The sensors of natural organisms produce measurement of the external environment. A more suitable analogy would be the sensors of a weather station, which simply measures temperature and air pressure at regular time intervals. While the information stream produced by this system could be treated as if it was a signal, this would be fruitless as useful information about the weather is simply not present. A weather forecast can only be produced by a system which has a weather model (which is an abstract representation of the atmosphere) and this model has to be fed by the input of hundreds or thousands of individual weather stations spread over a continent.
dendrite memory
we have no idea how neurons are storing information, how they are computing, what the rules are, what the algorithms are, what the representations are, and the like. [Michael Jordan, IEEE Spectrum]
Neural systems must store information. It is often suggested that the weights associated with either dendrites or synapses are a store of information.
Using an all-or-none pulse to code information is not unique to neurons. Optical media illustrates that there are two fundamental ways that data can be coded using all-or-none pulses: analog and digital. The latter approach has come to be much more common than the former, but nevertheless analog coding has in the past found specific applications where extremely high data rates had to be supported without the availability of high speed computing. Digital coding is shown in Figure 1. This is a temporal code where transitions code for a binary one and equivalent temporal periods without a transition code for binary a zero. The code is to a degree self-synchronizing due to a prescribed minimum and maximum number of zeros required between these transitions. The transition from a reflective to non-reflective region (a land and pit) may be seen as equivalent to an action potential. Each transition codes for a “1” for that temporal period, whereas if there is no transition in a specific temporal region then the code word is “0”. A digital code is very robust with respect to error, but it is inefficient. Figure 3 shows an analog code that uses the same all-or-none optical properties of a reflective medium but where information is coded by the distance between the transitions.
Neurons generally produce about 100 action potentials per second, but in some case are able to produce up to about 1000 action potentials per second. By comparison, an audio CD codes information in what appears to be very similar way – with each transition between “land”/“pit” being equivalent to an action potential. An audio CD is coded in such a way that a transition must be followed by a rest period that is at least 4 times the time period it takes for a single transition to occur, and also that the maximum time between transitions must be no more than 20 times the transition time (assuming that a transition takes up half of a given time period). This is a temporal digital code, where time periods with a transition represents a “1” and any time period without a transition represents a “0”. The data on an audio CD is organized into frames that represent 6 audio samples (using pulse code modulation), with each sample coded using 16 bits with 2 samples for every time period (for stereo sound). Each frame requires 192 bits for the audio data, but error correction and modulation extend this to 588 bits. The Audio CD format requires 44,100 audio samples per second and this leads to a bit rate of 4,321,800 bits per second ( 588 ÷ 6 = 98 × 44100 = 4321800). If a transition may be assumed to be half the time period of a single bit, then a 1 must be following by at least 2 zeros and by a maximum of 10 zeros. Therefore, an audio CD has a transition rate between one third and one 11'th of the bit rate (which is a rate up to 1,440,600 per second, with a lower bound of about 400,000). This is far in excess the rate at which neurons are able to produce action potentials; a difference of 3 orders of magnitude. Nevertheless, the bit-rate of the audio CD is considered by many audiophiles to be insufficent for human audio perception. As a result audio is often sampled 96,000 times per second or even 192,000 times per second, and at a resolution of 24 bits rather than 16. This is considered “high resolution” audio. The upper limits of the human auditory system have not been clearly established, and it may indeed be the case that the audio CD standard is sufficient to meet or exceed the abilities of human audition. Nevertheless, to code auditory perception using action potentials requires action potential rates at least two orders of magnitude greater than what is found in the neurons of natural organisms.
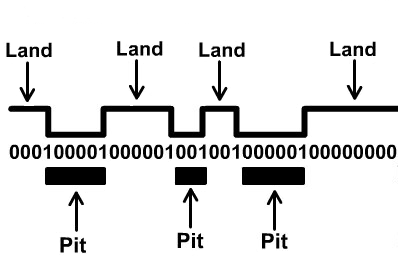
Figure 1 CD-ROM
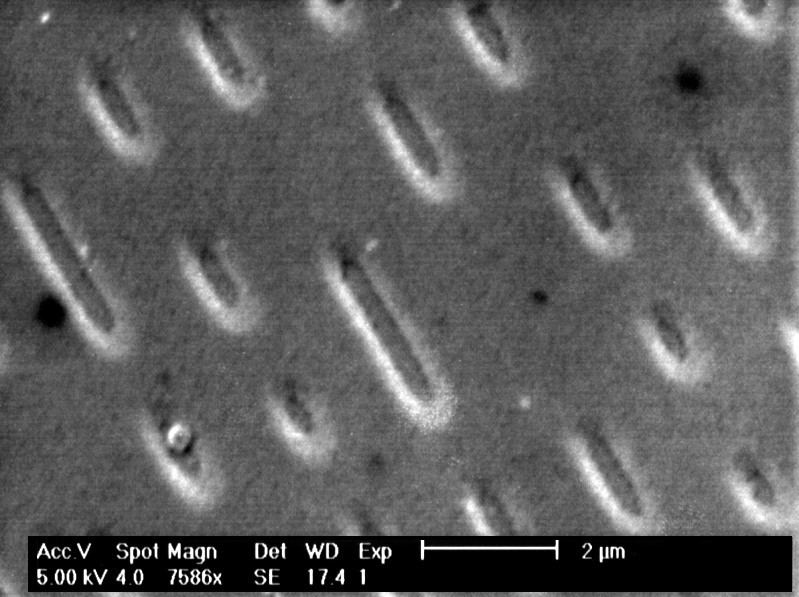
Figure 2 Scanning Electron Microscope image of CD-ROM

Figure 2 Pits and Lands overlayed with the time-code. Source: Giesbert Nijhuis

Figure 3 Laserdisc analog coding of wavelength by distance between transitions.
The spike code used by optical disc media demonstrates the principles by which information can be encoded on a physical medium. It is not a simple code where each land or each pit represents a zero or a one, or a code where the distance between pits represents a numerical value. One of the crucial features of the codes is that there is an upper and a lower limit to the spike rate. A naive code might represent a sequence of zeros simply by an absence of pits, and therefore an absence of spikes. This is undesirable for a number of reasons, one of which is that it is indistinguishable from nothing – the condition where there is no information. There is also an upper limit to the number of spikes that can be processed, and this should not limit the bit rate. In the case of the laserdisc, information is coded by the distance between spikes, but this is also more complex than a naive code, and is subject to the same restriction on a minimum and a maximum spike rate. Since the engineers of optical media faced similar problems in coding information as effectively as possible using just a single type of state transition it is likely that the neural code bears some relation to the optical media code. What the code for optical media demonstrates is that no matter how simple the code might appear, there may be considerable inherent complexity.
A criticism of making an analogy between digital computation and the function of natural neural system is that similar analalogies have been made in the past with respect to existing or new technologies, such as an analogy with hydraulic system or with telephone exchanges.
Figure 5 Image of the Intel 8008 die. Source: Ken Shirriff
Figure 6 Image of the Intel 8087 floating point co-processor die. Source: Ken Shirriff
The irony of neural systems when compared with digital systems is that the former relies on binary state action potentials whereas the latter relies on an electronic device whose primary function is to amplify analog signals, but yet it is neural systems that use binary repetition to support analog computation while transistors are restricted from a their natural analog state to two discrete states to support digital computation.
While it is undoubtedly the case that natural neural systems has over hundreds of millions of years evolved a wide variety of specialist functionality (in much the same way that the digital circuitry has over a century developed a wide variety so specialist functionality) the key to understanding neural systems is the central fact that they must support general computation. Computation has its orgin with calculation, and that is simply the ability to change numbers. Just as with digital computation, particular regard must be given to the history. Just as digital computation had it origins with integrated circuits comprising just a handful of logic gates, so too did distant organisms have neural circuitry consisting of little more than sensor neurons connecting to motor neurons. Some currently existing natural organism still have such exceptionally simple neural networks. These kinds of simple neural systems demonstrate that the fundamental role of a neuron is no more complex than a digital repeater.
Artificial neural networks are currently a very popular research subject and it is often claimed that they have a wide variety of useful applications. How exactly are they able to do anything useful? Often they are applied to image processing tasks, a domain in which it is difficult to establish the degree of usefulness. However, some researchers have claimed that they have developped artificial neural networks that are able to play games such as chess or go. To understand this in more detail it is useful to look at recent research describing efforts to allow systems that use neural networks to play traditional computer games (which among others games include chess). These are of course not neural networks that play the game itself, but they are used as helper functions alongside conventional algorithms which are implemented on digital systems. The neural network is in effect used as a kind of oracle to help a conventional algorithm with the decision tree of the game. An oracle which sells only snakeoil is not very useful, but an oracle that is able to play a perfect game of chess merits investigation. You can trick the eye by blurring images but you cannot cheat your way through a game of chess. So how exactly does this oracle work?
If we wish to play a game of chess we usually go about it by representing the chess board, code how the pieces move, and use an algorithm like the min-max to navigate our way through the decision tree. While this approach is effective for simple games such as tic-tac-toe, the decision tree for complex games such as chess is simply too large for this approach to be practical. In this way the system which employs these algorithms may be said to understand the game it is playing to some degree. But there is a very different way to approach the problems of building systems that are able to play the game. Rather than devising algorithms for the game ourselves, we simply observe games that are played and record the statistics. We take a picture of the game board at each turn of the game over many games (the learning period) and establish the probability of each move leading to a win, draw or loss. To save memory storage we blur the picture to the absolute minimum (that is, we reduce its resolution). This system is then purely an image processing and statistics gathering system. What it does is in effect build a decision tree in advance, rather than calculating it anew with each move. With any move a picture of the game board is taken and matched with the pre-stored database of images of game states. Given sufficient memory, this approach can certainly be effective. In fact, it can be applied not only to chess but to any turn-based game (or which can be seen as turn-based). But it is in effect a variation of the mechanical turk, which gave the illusion of a mechanical chess player when in fact there was a hidden human player. In this case there is human expert chess player hidden in the woodwork, instead the human expertise is hidden in a vast database of past games, especially that of the opening library. If that vast database is removed, the system would be unable to play in any meaningful way at all – it would fall back to a traditional algorithm, which in the simplest case would be selecting one of the possible moves at random (with the available moves being computed from the rules of chess rather than a neural network. Just as with the mechanical turk, once the illusion is broken, once the medicine is revealled as snake oil, it becomes pointless. If you know there is a hidden human, you would insist that he be removed before starting the game. In the same way, a human player cannot compete with an essentially unlimited statistical database that is accessed via a hidden network link. Without access to this database of low resolution images the system is able to play chess only in a trivial sense. This is reflected in the finding in recent research findings demonstrating the performance of neural networks playing traditional computer games. Most traditional computer games are very restricted in the ability to display graphical images, and generally present a static image, similar to a game board, on which game activity takes place. Performance on these games was shown to be approximately equal to that of a human player. Some games, however, presented a randomly generated background images and in these games performance dropped essentially to zero. This can be generalized across the field wherever an aritificial neural network approach is taken. Artificial neural networks can learn to recognize grandmothers but only when those grandmothers belong to an image dataset that is used to train the network. With novel images, performance drops essentially to zero. Alternatively, some images that appear to a human observer to be essentially randomly generated will be recognized as grandmothers by the network. These failures demonstrate that artificial neural networks are not oracles, and that there is no free lunch in computing. A grandmother cannot simply be detected or recognized, she needs to be represented. A grandmother consists of hair, teeth, eyes, skin and so forth, and these all need to be coded and represented. This is routinely done with computer generated animation – which is done entirely using conventional computing. A human artist will routinely look at a two-dimensional image of an object (even as complex as a grandmother) and will be able to generate the code from which that object can be represented and animated. We can say that an object has been recognized if the visual system has translated the information produced by image sensors back into the coded representation from which the object was originally produced. If the code matches then we can say the object has been recognized. How this system works in the human visual system is almost certainly using mathematical induction [ToyVision]. A system using induction has been shown to work with very simply visual environments – such as a two dimensional visual environment which consists only of triangles. Artificial neural networks do not produce any code associated with the representation of the objects which are intended to be recognized (and nor is there any scope for any such ability), and therefore what they do is not actually recognition at all. More accurately, it is simply a statistical image classification system, and put in those terms it is no more interesting than a mechanical turk.
... it’s important to distinguish two areas where the word neural is currently being used. One of them is in deep learning. And there, each “neuron” is really a cartoon. It’s a linear-weighted sum that’s passed through a nonlinearity. Anyone in electrical engineering would recognize those kinds of nonlinear systems. Calling that a neuron is clearly, at best, a shorthand. It’s really a cartoon. There is a procedure called logistic regression in statistics that dates from the 1950s, which had nothing to do with neurons but which is exactly the same little piece of architecture. [Michael Jordan, IEEE Spectrum]
Our brain is a small lump of organic molecules. It contains some hundred billion neurons, each more complex than a galaxy.
[Gardiner on Hofstadter]
The relay is a remarkable device. Its a switch, surely, but a switch that turned on and off not by human hands but by a current. You can do amazing things with such devices. You could actually assemble much of a computer with them. [Petzold, Code: The Hidden Language of Computer Hardware and Software]
The evolution of systems we design and build that are capable of computation also begins with the humble relay. One of the earliest ways to transmit information also uses a coding system similar to that of the CD. Morse code is less similar to the neural code in that information is represented by more than a single event, a spike in the case of neurons and a transition in the case of optical media. With Morse code information is represented by a spike like event, but this spike can have two states – long and short, typically represented as ‘dot’ and ‘dash’. Sequences of dots and dashes represent letters of the latin alphabet (or arabic numerals). Temporal distance between a dot or dash is used to represent where an individual letter begins and ends or where a sequence of letters begins or ends. While Morse code is largely obsolete and has not been used in any of the systems developed to support digital computation it continues to be used in a small number of applications, mostly in military communications in times when radio silence is important. In the past, however, Morse code was the only way to quickly and reliably transmit information over long distances (thousands of kilometer). The simple technology of the time, however only allowed the physical signal to propogate over relatively short distances (a few hundred meters). This is precisely the same problem that neurons have faced in the distant evolutionary past. One stop-gap method is to carefully insulate your conductor, and in the case of the technology that enabled telegraphy, this extended the distance by two orders of magnitude (to a few hundred kilo-meters). Neurons also developed insulation, in the form of glial cells that are especially oily and which can form themselves into very thin sheets that wrap themselves around the axons of neurons, especially for neurons which have axons that extend themselves over longer distances. What is interesting about Morse code is that its simple on-off structure and the need to communicate over longer distances led to the development of the relay. The purpose of a relay is simply to repeat the code, but it does so automatically. However, despite being a very simple innovation, a relay allows for the development of most of what is required for general computation. In the development of neural system, therefore, the fudnamental advances are the development of a code that is suitable for being transmitted over long distances and the ability for neurons to relay or to repeat this code without any loss of information. These two abilities enable information not only to be transmitted and received but for it to be processed. As the history of analog electronics demonstrates, a wide array of complex behaviour can be produced using just the simple relay. A revolutionary change from analog to digital has largely brought an end to the era of analog systems, but in the history of natural neural system it is gradual evolutionary change rather than revolution that predominates.
Cellular automata such as Conway's Game of Life show that general computation can be achieved by systems that are very different from a Von Neuman machine with its list of stored instructions and central memory. While systems of computation implemented on cellular automata might not be very paractical, such a system would be very difficult to decypher purely from observing the hardware which stores the cells change state .