Sudoku is a popular constraint-based puzzle game. For human players it is intended as a logic puzzle which is solved by recognizing the logical relationships and necessities implicit within a specific starting grid. Despite the fact that the game has been created for human entertainment precisely because it is enjoyable (for most humans) to discover the logic of a specific game, an analysis of the game by mathematicians tends to ignore the inherent local structure and focus instead on redefining the problem in terms of formal systems that in some way optimizes the solution space. Computer algorithms designed to solve sudoku typically mirror this mathematical approach.
A particularly concise conventional solution to sudoku can be found in the computer programming language Prolog. This is a language in which programs consist of relationships specified in logic rather than as a temporal sequence of specific instructions that relate to the underlying architecture of the system.
sudoku(Rows) :-
length(Rows, 9), maplist(same_length(Rows), Rows),
append(Rows, Vs), Vs ins 1..9,
maplist(all_distinct, Rows),
transpose(Rows, Columns), maplist(all_distinct, Columns),
Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
blocks(As, Bs, Cs), blocks(Ds, Es, Fs), blocks(Gs, Hs, Is).
blocks([], [], []).
blocks([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
all_distinct([N1,N2,N3,N4,N5,N6,N7,N8,N9]),
blocks(Ns1, Ns2, Ns3).
problem(5,
[[9, _, 7, 6, 5, 4, 3, 2, 1],
[_, 4, 6, 1, 7, 3, 9, 8, 5],
[_, 5, 1, 9, _, 8, 7, _, 6],
[_, _, 8, 5, 3, 7, 6, 9, 4],
[_, _, _, 8, 9, 2, 1, 5, 7],
[_, _, _, _, 6, 1, 8, 3, 2],
[_, _, _, _, 8, 6, 4, 7, 3],
[_, _, 2, _, _, _, _, _, 8],
[_, 6, _, _, _, _, _, 1, _]]).
In this particular implementation, for convenience and readability, puzzle grids are hard-coded as facts. A sudoku grid is stored as a list of lists, with each list representing a row. Some Prolog list manipulation functions can treat this as a two-dimensional matrix. Unknown cells of the grid are coded with an underscore, which in Prolog represents an anonymous variable. The task for the program is to instantiate each variable with a specific number in the range between 1 and 9. If there is a unique solution, a query posed on a 9×9 matrix resolves with all the variable instantiated and thus solves the sudoku puzzle.
problem(5, Rows), sudoku(Rows), maplist(portray_clause, Rows).
A conventional procedural algorithm for solving sudoku is shown below. This is a simply an exhaustive search, which requires no ‘logic’ at all.
x←0
for i←1 to n do
for j←1 to n do
for k←1 to n2 do
grid [n(i − 1)+ j ][k]←x(mod n2)+ 1
x←x + 1
x←x +n
x←x + 1
The program in Prolog appears quite different from the nested loops carried out by the conventional basic (or ‘root’) algorithm. In fact, a ‘program’ written in the Prolog programming language can be somewhat difficult to understand in comparison. The core of the Prolog program is, however, not that difficult. The key element of this program is the all_distinct list function, which returns true if all the elements of the list are unique. Prolog does not just carry out a simple conditional test, but rather uses rules of inference to find a possible match for any uninstantiated variables that might be present in the list. In sudoku each row, column or block must have all the numbers in the range between 1 and 9, with each number occuring only once. This is a constraint, and the all_distinct function implements the uniqueness constraint. If we constrain a single variable in a 9 element list in this way then a single variable can be matched with the missing number. In this way, the all_distinct function instantiates any variables (either named or unnamed) if it can and returns the list with missing elements filled in. A list may be returned complete, partially complete or without any of the missing elements completed.
A query for distinctness on an incomplete list:
Vs = [9, _, 7, 6, 5, 4, 3, 2, 1],
Vs ins 1..9,
all_distinct(Vs).
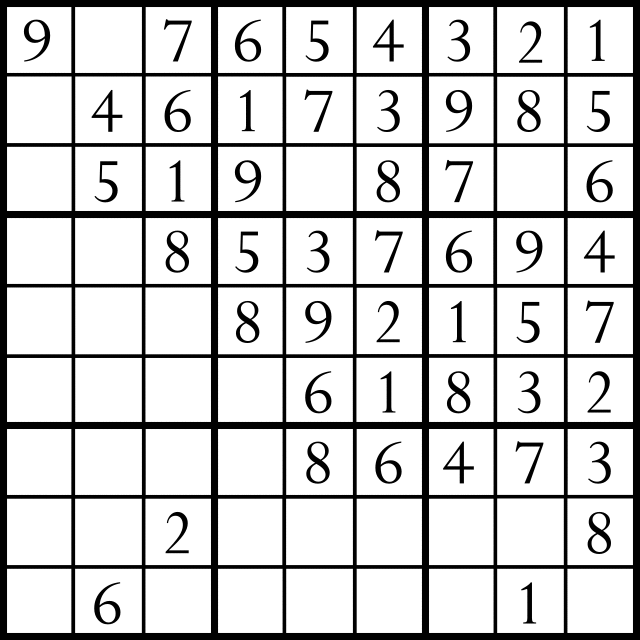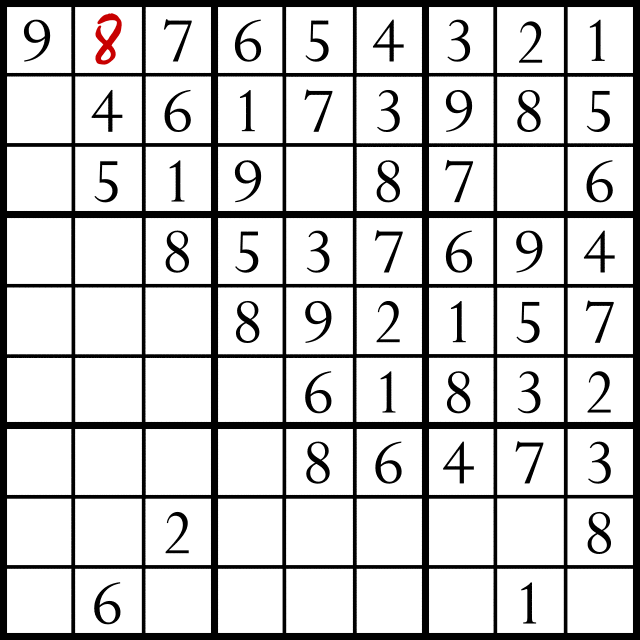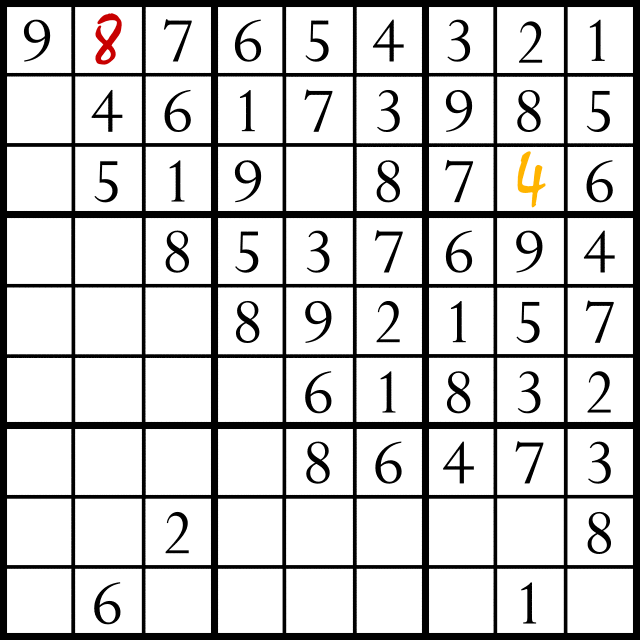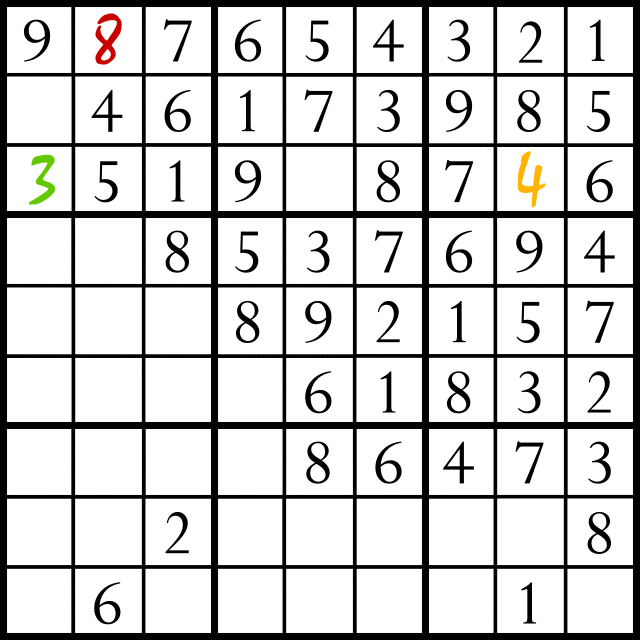
The query above produces the completed list, with the anonymous variable instantiated with the number 8. This may be referred to as an inference, in this case a trivial deductive inference. What can be inferred depends on the rules, and in the case of sudoku a small set of rules allows a 9×9 array to be completed from a very sparse original state. A unique solution can be found with as few as 17 elements of the array complete, which means that a game grid can be almost 80% empty and it can still be solved using just a few simple rules.
Vs = [9, 8, 7, 6, 5, 4, 3, 2, 1].
Prolog queries are implemented primarily as this type of search for an unknown, constrained by a set of logical rules. In the example above, the program simply searches through all the values that the unnamed variable could have and finds that the all_distinct predicate holds true only for the value 8. This is the core algorithm for Sudoku. Sudoku is implemented simply as a two-dimensional version of this search. A transpose allows the columns to be searched and a 3×3 blocks transform allows the blocks to be searched. This algorithm is merely a constrained exhaustive search and fundamentally no different than the conventional procedural algorithm. Prolog allows this search to be specified ‘logically’ but the program itself is blind to the logic of sudoku.
Since sudoku is logic puzzle game specifically designed for human enjoyment, it is not enough for a sudoku program to find the solution in the most efficient way possible but rather it should find the logic that leads to the solution. The approach to solving sudoku should therefore be similar to the approach taken by a human sudoku player. Solving sudoku in this way may lead to a more general understanding of the computational systems which underpin our mental function.
To understand any system of computation it is often very helpful to gain an understanding of the algorithms employed by that system, something which can sometimes be gleaned from the overall behaviour of the system. Natural neural systems are no different. They may be difficult to understand, but if there is a specific function that this information processing system is known to perform and it can be shown that this function can only be performed in one way then we may say that we are able to understand that specific element of how that systems functions. In this way we can with certainty know and fully understand elements of neural systems without understanding anything about the underlying implementation of those systems. Indeed, we can be entirely ignorant about neurons, action potentials, synapses and all the ensuing complexities of neural architecture but nevertheless by using inductive reasoning about the macro-function of the system as a whole we can know what that neural system must be doing.
As an example, we know with certainty that all visual information is the product of two 2-dimensional retinal sensor arrays. Any 3-dimensional information must therefore necessarily be reconstructed from the projected disparity of objects on the two sensor arrays. This is evident from the fact that we can directly perceive the loss of 3-d information by simply closing one eye. Calculating the distance to an object from the disparity on the sensor array can be done only one way – by triangulation. It is a simple inverse relationship between the baseline distance between the sensors, the focal depth and the disparity (f×b/d)1. Calculating the distance requires division. This is not a trivial division that can be implemented by a shift register and neither is it relatively straight forward integer division. The human visual sensor array is very small, and this requires a very precise measurement of disparity and therefore great precision is necessary to calculate distance effectively. The precision may be estimated by the difference between the disparity the sensor system is capable of discriminating and the ability to perceptually estimate distance from perception. For a digital system, this depth calculation would have to be done essentially for every pixel of every frame, which for a real-time visual processing could easily exceed the abilities of processors capable of processing billions of operations per second. We know from practical implementations of digital computation that division is the most difficult of the basic arithmetic operations, requiring repetition and taking up to 1000 times as long as addition or subtraction. We also know that it is very difficult for a conventional model of a neuron to perform useful high precision division. Given that it has taken half a century of intensive active development to decrease the time difference between an addition operation and a division operation from three orders of magnitude to one order of magnitude it would seem reasonable that a similar type of evolutionary quest for the most efficient way to perform division may well have taken place in the evolutionary development of neural systems. By contrast with the evolution of the microprocessor, which currently has available to it billions of cycles per second over 10 or even 100 cores, it is also known that neural systems are by comparison very slow. This should place an additional emphasis on the need for neural systems to have access to efficient division. In spite of the almost self-evident importance of efficient precise division in much of the activity of natural neural systems the subject of division is almost entire absent from the body of literature that seeks to explain how neural system work. This body of literature consists almost entirely of the many and varied theories about how a neuron might recognize or learn, with little if any backward glance at the seemingly humble problem of division. This is in spite of it being well known that any computational activity must necessarily rely on division and that many of the activities of natural neural system clearly indicate the need for division. Investigating how division may be carried out efficiently is therefore likely to inform us considerably on many aspects of natural neural systems, in particular the problems involving the processes that underly perception. Simple, straight-forward reasoning from known facts about how a complex neural system functions can therefore readily lead to conclusions about how these systems must function. Not only can we know how the system must calculate depth information from a disparity on the sensor arrays but we can also know something about how arithmetic as a whole must be implemented on those systems.
Just as the fundamental problem of division is almost entirely absent from the literature on neural systems (even artificial neural systems), a ‘logical’ approach is equally absent from the literature on sudoku. It is not entirely clear why this should be. After all, the Prolog programming language has been designed specifically for its ability to specify problems in logic rather than computation. Perhaps it is because the code is inelegant or because the approach is ‘obvious’ and therefore seemingly not interesting. Or alternatively, perhaps the unintuitiveness of specifying a problem in the underlying logic of our own mind naturally drives the programmer toward the traditional approach. While this approach efficiently solves sudoku puzzles, it is not helpful to understanding the underlying mechanics of natural neural systems. Just as it is not helpful to solve a sudoku puzzle by a simple brute force search because that contradicts the purpose of the game, it is equally unhelpful to take this type of approach to understanding natural neural systems. It is instructive, therefore, to examine a more ‘logical’ approach to systematically coding the underlying logic of our intuition. Sudoku is interesting in this respect because it serves as a very simple formal problem that illustrates more broadly how some aspects of our neural system must function.
The first issue to examine with respect to sudoku is one of interpreting the problem space. The conventional approach views the game array as a space to iterate through in view of the constraints of the game. A human player would not take this view. A human player would look for empty positions on the grid which can be completed due to logical necessity. The simplest rule is to look for any row, column or block that has only one missing number. If there is only a single missing element then the all_distinct function will fill in the element that is missing (see the all_distinct list query above). Once we have carried out this very basic step, it is apparent that there may now be rows, columns or blocks that could not previously be solved but due to the positions that were filled in by the last step can now be completed. We proceed by filling in what we can and then we start again with the newly updated grid as if it were a starting grid. This is inherently a recursive approach. We have a simple set of rules, which we repeat until we reach and end-state. For sudoku the set of rules specify the logical conditions when we can fill in an empty space. For Prolog, this means that a variable is instantiated. We continue until either the game grid is complete or if the game grid is unchanged from one iteration to the next. If there is no change then this means the problem cannot be solved with the current set of rules. The way we can view the game grid is therefore as a set of facts which have been asserted. We recursively apply a set of rules to those facts until we either have a solution or a failure to find a solution. This is not strictly true of this particular implementation of the game grid as list because each ‘fact’ is not asserted independently. Nevertheless, it is useful to see it like this because more complex systems can be built where truly independent facts can be asserted.
problem(5,
[[9, _, 7, 6, 5, 4, 3, 2, 1],
[_, 4, 6, 1, 7, 3, 9, 8, 5],
[_, 5, 1, 9, _, 8, 7, _, 6],
[_, _, 8, 5, 3, 7, 6, 9, 4],
[_, _, _, 8, 9, 2, 1, 5, 7],
[_, _, _, _, 6, 1, 8, 3, 2],
[_, _, _, _, 8, 6, 4, 7, 3],
[_, _, 2, _, _, _, _, _, 8],
[_, 6, _, _, _, _, _, 1, _]]).
In more complex dynamic fact spaces the rules transform an initially simple but numerous set of facts to more complex but less numerous facts. The game of sudoku does not require the transformation of any facts as it requires only the missing elements to be completed. Nevertheless, we may illustrate transformation rules in a case where a transcription error has produced an invalid game state. A rule could be introduced which does not just instantiate variables but which removes or swaps an entry if an error condition is met. The corrected game grid can then be tested (recursively) to determine if it can be solved. If a solution can be found then the correction is accepted.
sudo(R) :- maplist(findone(_),R,F1),
transpose(R,C), maplist(findone(_),C,F2),
blocklister(R,B), maplist(findone(_),B,F3),
maplist(findone(R),R,F4), maplist(findone(C),C,F5),
sudo(R,[F1,F2,F3,F4,F5]).
sudo(R,F) :- a_one(F),
writeln(recursing), maplist(portray_clause,R),
sudo(R), !.
sudo(_,F) :- not(a_one(F)).
blocklister(R,C) :- blocklist(R,S), append(S,T), threedechop(T,C).
blocklist([],[[],[],[]]).
blocklist([R1|R],[[T1|B1],[T2|B2],[T3|B3]]) :-
threechop(R1,[T1,T2,T3]),
blocklist(R,[B1,B2,B3]).
threechop([],[]).
threechop([L1,L2,L3|L],[[L1,L2,L3]|T]) :- threechop(L,T).
threedechop([],[]).
threedechop([L1,L2,L3|L],[T|R]) :- append([L1,L2,L3],T),
threedechop(L,R).
:- use_module(library(clpfd)).
findone(_,L,_) :- maplist(integer,L), write(complete),!.
findone(T,L,I) :- findmyint(T,0,L,L,I), !.
findone(_,_,0) :- write(fail).
findmyint(_,_,_,[],_).
findmyint(T,K,M,[L1|L],I) :- integer(L1), K1 is K+1,
findmyint(T,K1,M,L,I).
findmyint(_,_,M,[L1|_],1) :- var(L1), L1 in 1..9, all_distinct(M),
integer(L1), !.
findmyint(T,K,M,[L1|_],1) :- not(var(T)), var(L1), K1 is K+1,
L1 in 1..9, transpose(T,TT),
nth1(K1,TT,MT), clear_var(MT,MTT),
clear_var(M,M1), append(MTT,M1,M2),
clear_dup(M2,M3),
all_distinct([L1|M3]),
integer(L1), !.
/* a test for integer stops speculative testing*/
clear_var([],[]).
clear_var([L1|L],[L1|L2]) :- not(var(L1)), clear_var(L,L2).
clear_var([L1|L],L2) :- var(L1), clear_var(L,L2).
clear_dup([],[]).
clear_dup([L1|L],[L1|L2]) :- not(member(L1,L)), clear_dup(L,L2).
clear_dup([L1|L],L2) :- member(L1,L), clear_dup(L,L2).
a_one([]) :- false.
a_one(L) :- integer(L), L==1, !.
a_one([L1|_]) :- not(var(L1)),a_one(L1), !.
a_one([_|L]) :- not(var(L)),a_one(L), !.
range(A,A,A).
range(A,B,C) :- A
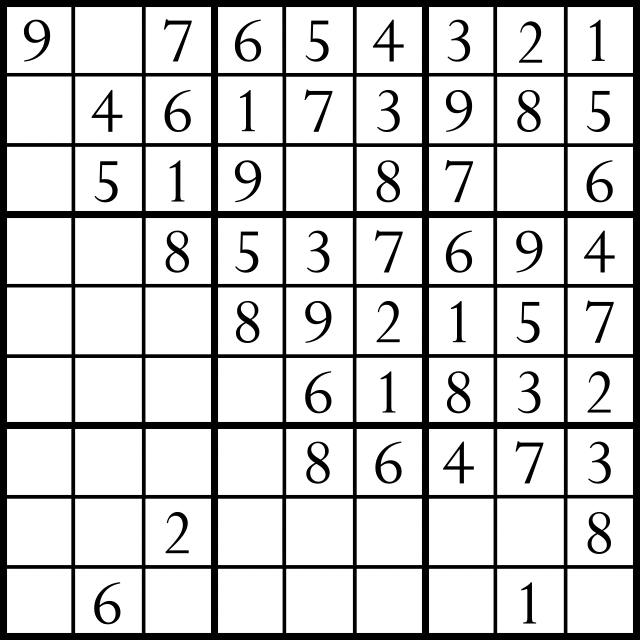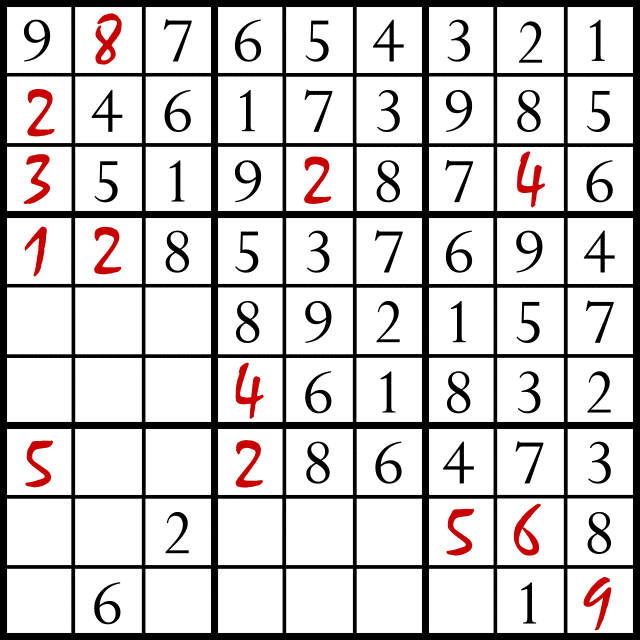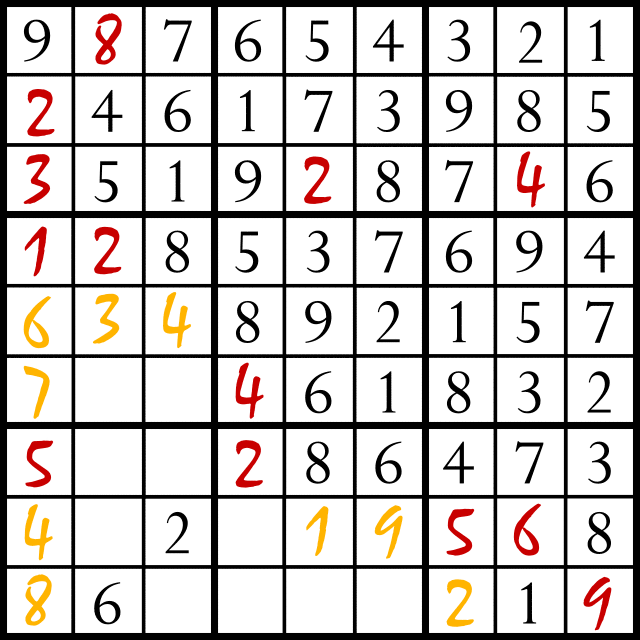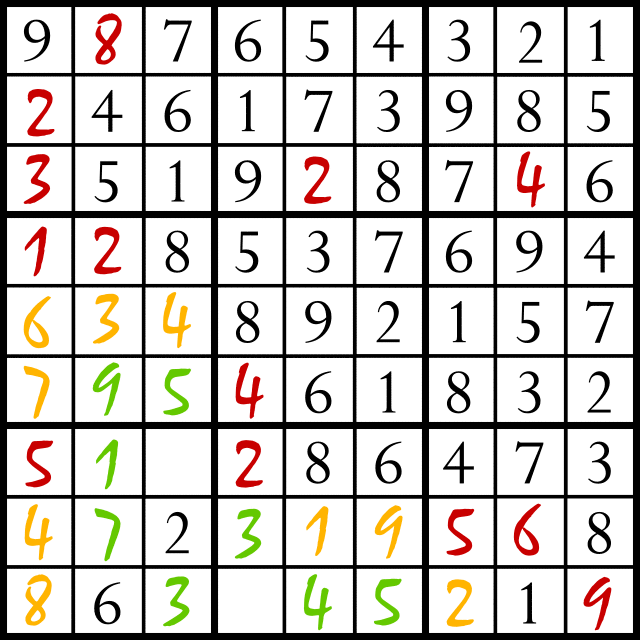
Having developed the core of a sudoku solver, which simply recurses through each element in a list (of row, column or block) and tries to instantiate a variable if it is the only variable in that list (by imposing the all_distinct function) we wish to define a sudoku solution as a list of logical heuristics (or ‘strategies’) which match those of a human player. The purpose is not to develop a complete sudoku solver but rather to demonstrate the correct approach to building a sudoku solver whose approach approximates that of a human player. Filling in a single empty block is a trivial step and not particularly instructive. Nevertheless, it is sufficiently constraining to complete the game if a speculative search is allowed. To allow additional heuristic rules to have effect it is necessary to turn off speculative completion. The simplest non-trivial rule is to check two rows or columns for identical entries and then cross check that with the three elements of the opposing block where the third identical entry must reside. If those three grid locations are constrained by two existing entries then the third entry must be the identical entry that was previously found. The code below implements this by checking all the combinations of rows for a given block (3 rows) for numbers that are equal. This is straight forward to do with the nth0 function, which allows the n'th element of a list to be selected. Then we need to find the 3'rd row of the block which does not have the identical number found, then select the correct 3 elements of the row that belong to the block. This works but the code is not very elegant. It is possible that that this could be expressed more succinctly. Nevertheless, it is a simple but non-trivial rule and it demonstrates how we would add rules to the system to make it more complete. A set of rules may be considered to be complete when they are able to solve all possible sudoku puzzles that are able to be solved without taking a speculative step.
crosscheck(R,H) :- LB is (H*3), UB is (2+H*3), range(LB,UB,L),
nth0(L,R,L1), M is LB+((L-LB+1) mod 3),
nth0(M,R,L2),int(L1,I,PI),int(L2,J,PJ),I==J,
N is LB+((L+2) mod 3), nth0(N,R,L3),
clear_var(L3,LL3), not(member(I,LL3)),
BK in 0..2, BI is floor(PI/3),
BJ is floor(PJ/3), all_distinct([BJ,BI,BK]),
threechop(L3,XXX), nth0(BK,XXX,YYY),
member(I,YYY), clear_var(YYY,YYY),
write(found_an_), write(I), write(' '),
write(in_row_), write(BK),write(' '),
write(for_block_),writeln(YYY).
While traditionally the sudoku game grid is represented as a 9×9 array, this array is generally quite sparse in the initial state.
problem(4, [[9,_,_,_,_,_,_,_,_],
[_,_,_,_,_,3,_,8,5],
[_,_,1,_,2,_,_,_,_],
[_,_,_,5,_,7,_,_,_],
[_,_,4,_,_,_,1,_,_],
[_,9,_,_,_,_,_,_,_],
[5,_,_,_,_,_,_,7,3],
[_,_,2,_,1,_,_,_,_],
[_,_,_,_,4,_,_,_,9]]).
A more efficient representation can be achieved in Prolog by asserting only cells which have entries in them. These can be considered the original facts (or ground truth) for the system.
assertz(sga(1,1,9)),
assertz(sga(6,2,3)),assertz(sga(8,2,8)),assertz(sga(9,2,5)),
assertz(sga(3,3,1)),assertz(sga(5,3,2)),
assertz(sga(4,4,5)),assertz(sga(6,4,7)),
assertz(sga(3,5,4)),assertz(sga(7,5,1)),
assertz(sga(2,6,9)),
assertz(sga(1,7,5)),assertz(sga(8,7,7)),assertz(sga(9,7,3)),
assertz(sga(3,8,2)),assertz(sga(5,8,1)),
assertz(sga(5,9,4)),assertz(sga(9,9,9)).
Once the available facts have been asserted, the logic of the system can then be applied to those facts. The purpose of these rules is to discover new facts that have logical necessity. These are then asserted alongside the original facts. Not only can we assert concrete facts (integers) but we can assert constraints. For example, we discover that grid location (3,1) must contain a 7, but grid location (2,1) we can have any integer except 9, and at grid location (9,1) the constraint is 3,5 and 9.
assertz(sga(2,1,1..8)).
assertz(sga(3,1,7)).
assertz(sga(4,1,1..4\/6..9)).
assertz(sga(5,1,3\/5..9)).
assertz(sga(6,1,4)).
assertz(sga(7,1,2..8)).
assertz(sga(8,1,2)).
assertz(sga(9,1,1..2\/4\/6..8)).
sga(9,1,X).
X = 1..2\/4\/6..8.
sga(9,1,X), A in X, A=2.
X = 1..2\/4\/6..8,
A = 2.
sga(9,1,X), A in X, A=3.
false.
Not only can we discover new facts, but with sufficient discoveries we can complete entire rows. Once an entire row is complete, we can retract all the individual facts that make up that row and then assert the row as a list of its elements.
retract(sga(1,1,9)).
range(2,9,X), retract(sga(X,1,_)).
assertz(sga(1,[9, 8, 7, 6, 5, 4, 3, 2, 1])).
Once all the rows are complete, we retract all the rows and assert the entire grid (as a list of rows).
assertz(
sga(
[[9, 8, 7, 6, 5, 4, 3, 2, 1],
[2, 4, 6, 1, 7, 3, 9, 8, 5],
[3, 5, 1, 9, 2, 8, 7, 4, 6],
[1, 2, 8, 5, 3, 7, 6, 9, 4],
[6, 3, 4, 8, 9, 2, 1, 5, 7],
[7, 9, 5, 4, 6, 1, 8, 3, 2],
[5, 1, 9, 2, 8, 6, 4, 7, 3],
[4, 7, 2, 3, 1, 9, 5, 6, 8],
[8, 6, 3, 7, 4, 5, 2, 1, 9]]
)).
This then may be considered a system for solving sudoku whose approach is similar to that taken by the visual systems of natural neural systems. We take an input that is very sparse and by a set of rules and relationships this input is transformed systematically and repeatedly in the same way as we would solve a puzzle and in so doing we find ‘solutions’ that may be considered abstract representation of the external environment. What is notable about a logical implementation of sudoku is that we do not need to precisely specify an initial array which represents the game. We can simply assert facts, which in the case of natural neural systems would arrive from the sensors. An array requires every position within that array to be defined (even if by a placeholder variable as in Prolog). Facts can be asserted ad-hoc and the array structure is implicit from those facts and the logical rules which operate on them. If those rules are general enough, then the system will not simply be restricted to a single size grid but will be able to solve related puzzles of different sizes.
One aspect of solving a problem like sudoku using a constrained logical search is that simple logical rules often lead unexpectedly to run-away solutions. This can be very seductive in that a set of just a few rules can lead to a complete solution. Not only does setting the constraint in the three dimensions of sudoku (rows, columns and blocks) lead to a run-away solution but the rule of completing a single empty element in an otherwise complete row or column also leads to a complete solution of the game. To stop this speculative completion we can add a test in the code to check to see if a finding is real or speculative (in this case, testing a variable to see if it has been instantiated). The rules that lead to run-away solutions tend to be very simple, whereas the logical heuristic rules by which human players solve the game can be quite complex and intricate to specify (although they appear to us intuitively as simple and logical). Why then go to the trouble of specifying complex rules when just a few simple rules will solve the whole game? There is some evidence that that natural neural systems may also have difficulty with this same question.
There are some humans who seem to have extraordinary abilities in exactly the kinds of problems that can be solved a short-cut in the logic that leads to run-away solutions in Prolog. Known as savants, these individuals can recite whole novels verbatim from memory, search entire libraries of books as efficiently as a search engine, or solve mathematical problems as quickly as a computer. Associated with these almost oracle-like skills is invariably some debilitating neurological disability. These abilities are not the equivalent of a trick or illusion. They are remarkable because the problems they are able to solve truly requires the equivalent of a super-computer. Of course there are limits to these abilities. No savant has ever been observed with abilities that contradict the limits of computation. In the past the ability to memorize entire libraries might have seemed extraordinary, but now that we have the ability to store this information on a memory card that is almost microscopic, this ability seems less magical than it once might have. A savant may be able to calculate the day of the week from an arbitrary date, but so can a calculator using a fairly straight forward but perhaps slightly unintuitive equation. However, no savant has ever been found who is able to solve more complex games such as chess or sudoku in time frames so small that they appear to solve the problem instantaneously. There have been chess masters with savant-like abilities, who can perform a variety of chess-like ‘tricks’ to entertain an audience, such as playing 10 naive games of chess at the same time (with almost instantaneous decision times) or recognize a specific historical game from seeing just one game position. While individuals with these abilities can be trained (or train themselves) to be excellent chess players their decision time when playing against an expert is far from instantaneous. In fact, they may often be observed to be struggling with the clock, which sets a strict limit on the time allocated. The existence of formal chess tournaments has allowed the games of some of these individuals with extraordinary skills to be studied in forensic detail. One of the observations has been that the rapid-fire games against naive players is much less successful with expert players, and for the individual to succeed he has had to adapt his style of play to be less spontaneous and more thoughtful.
The paradox of the savant is how such extraordinary ability can exist at the same time as a terrible debilitating neurological disability (which are typically so great that the individual would have no chance of survival in their natural environment). The clue to resolving this contradiction is that these individuals with extraordinary ability invariably are not aware how they solve the problem on which they exhibit such seemingly great ability. The solution simply appears to them, in the same way that a Kanizsa triangle can be seen to appear to a normal human observer from simple pac-man like shapes or that a number seems to appear from randomly coloured dots in an Ishihara colour blindness test. Attempting to solve sudoku with a symbolic system capable of completing a sparse game board using logical induction (in this case the simple rules of heuristic deduction) leads to an important insight about such systems. They need necessarily to be implemented as a constrained search, and the ‘logic’ element which lies as a layer of abstraction above the lower level search element in many ways restricts the search to the rules of the ‘logic’. If this restriction is removed, then the search is able to rush to completion without regard to the logic. This can appear as extraordinary ability. Even in Prolog, a few statements setting out the constraints can appear extraordinarily able. However, in light of the need to understand the logic of a solution rather than finding the solution itself, this ability begins to appear more of a liability than ability. It prevents the logic from working, and instead relies entirely on the constrained search. If natural neural systems use systems of logical induction, and this system also relies on constrained search, then it is quite possible that it would also suffer from this particular problem. A system in Prolog that applies the logical heuristic rules on deduction which human players use to solve the game is only as able as the set of rules it relies on. Each rule may be difficult and complex to specify and together they may only solve problems that are ‘easy’. We may imagine that this system is damaged in some way that removes what is in effect a ‘reality check’. We can see that if a single check is removed, then a system that slowly and laboriously moves step by step to a solution (which often then fails along the way if the problem is too ‘hard’) is transformed into a system that almost instantaneously finds a solution no matter how difficult the problem. However, this system will necessarily fail to report what the logical steps are by which it arrived at the solution. This failure is the key to understanding the problem. Marvelling at the extraordinary ability of a savant is fundamentally no different than naively marvelling at the high revs an engine is able to achieve when the link to the drivetrain has been damaged. Indeed, a fairly ordinary engine can achieve race-car levels of rpm without any load, but it is not thereby magically transformed into a real-world race car. In fact, it will have great difficulty in functioning at all, and will in effect be disabled. The seemingly extraordinary abilities of the savant can be understood as this kind of deficiency, not of a combustion engine but instead of a logical inference engine. This then resolves the paradoxical abilities of the savant. The ability is simply the product of a restraint removed from the underlying system. This restraint is necessary for the overall system to produce useful real-world results. With the restraint removed, individual problems that have a formal structure that can be resolved by a simple constrained search can be solved very quickly, but for complex problems which may rely on the logic of a variety of more simple problems, performance will fall to nominal levels. Natural neural systems of course do not have an external agent to code this logic for them. It has to be painstakingly developed and tested. In this way we can learn and develop, perhaps using games such as chess or sudoku as touchstones to help us guide the way. Perhaps that is why we enjoy these types of games, because they help us build up a reservoir of useful heuristic logic that can then be employed in solving much more complex real-world problems. To a savant, however, a game such as sudoku is not a helpful stepping stone but rather an end-goal in itself. The savant will seem to have extraordinary ability in respect of that particular game, but he never learns and progresses, but rather remains in a child-like state with a small set of extraordinary abilities, about which he is remarkably uninformed.
The importance of sudoku in relation to other similar games is the requirement of logical certainty. With other related deterministic board games such as chess or go a human player has a similar need for logical certainty but is rarely able to find it. Although games such as chess or Go are games in which two players oppose each other, the game progression may be viewed formally in the same way as a sudoku puzzle progresses. Progression is simply the application of a set of rules, which in the game of chess are the rules that define how the pieces may move and in the game of go it is the rules which govern where the game pieces may be placed. Both chess and Go are much more complex than sudoku and cannot be played by either by logical certainty or exhaustive search. Sudoku by contrast may be considered solved by a conventional constrained search. This is because the game space is relatively small and always starts by being partially complete, and in addition as the puzzle is progressively solved the search space declines. For chess, the board becomes less populated as the game progresses and as a result the search space expands exponentially. The game of Go is more similar to sudoku in that the board becomes increasingly populated as the game progresses and as a result the search space declines. However, the most common game board for Go is much larger, consisting of 361 spaces compared to 81 for sudoku, all of which are empty at the start of the game. As a result, a human player is only rarely able to find logical certainty when deciding on move. In the worst case a player may proceed simply by choosing one of the possible moves at random. This is the solution employed by all current game-playing algorithms. For sudoku this amounts to a constrained brute force search. For chess and the game of Go the search space is far too large and therefore a variety of methods to constrain the search space are employed. The most common ways to constrain the search is either with a heuristic or a probabilistic evalution function. An evaluation function recursively back-propogates a numerial evaluation of the board as far forward as the compuational abilities of the system will allow whereas a probabilitic function is produced using a statistical evaluation of past games.
Irrespective of how the search space is trimmed with respect to the evaluation function, an exhaustive search is equivalent to a random choice. Not only is there no logical necessity in the choice, but there is no potential for logical necessity. A human player, by contrast searches for logical necessity but due to the complexity is unable to articulate the logic by which he makes his decision. Which is complicated by the fact that a human player can and does makes decisions by a variety of means, including heuristics and random choices. What sudoku demonstrates is a system where the logic employed by human players can be expressed explicitly and can be formulated within a logic programming system such as Prolog. Sudoku is not so simple so as to be trivial for a human player but on the other hand it is not so complex that we are forced to find speculative solutions. Solving sudoku, therefore, gives us insight into solving more complex games using the same logic. More complex logic is often expressed as ‘goals’ or abstract aims (such as attack or defence). In sudoku the goal
There are many ways to understand the function of natural neural systems. Just as the game of sudoku was developed as a game designed to hone the skills of logical reasoning, equally it has important implications for understanding reasoning systems themselves and the means by which we should proceed step-by-step to advance that understanding. Sudoku illustrates that not only are there no short-cuts to understanding natural neural systems, but also that short-cuts can be dangerous traps which can debilitate our ability to reason effectively. Like a minimal sudoku puzzle, our current understanding of natural neural systems currently consists of mostly empty space. Each space has to be filled using logical reasoning that demonstrates necessity rather than speculation. And like even the most difficult game of sudoku, which we know can be solved by the application of a simple set of logical rules each of which we already know, so too we currently know all the essential facts necessary to understand how natural neural system function. We know that neural systems are systems of calculation and computation and in the past century not only have we designed and built complex systems ourselves, but we have developed a detailed general theory of computation. We have also constructed complex logical programming paradigms such as Prolog which were specifically designed to allow problems to be defined using formal logic than by the mechanics of the underlying system. While Prolog is generally seen presenting a ‘pure’ logic programming paradigm it was seen initially only as a first step toward the goal of developing an effective paradigm of programming in logic. Natural neural systems have been evolving for hundreds of millions of years. If induction systems are an important component of the function of natural neural systems, then it is likely that it developed in an early simplified and approximate form which has been refined over time. Prolog may be viewed in this light; an early but yet unrefined attempt at building systems capable of filling in the many blank spaces that any system which aims to accurately model the external environment from limited sensor input.
Sudoku inherently has a grid structure, but a visual representation of the external environment is inherently three-dimensional. The facts from the visual sensor array will have an associated two-dimensional coordinate but the geometry that this must map towards is in three dimensions. One of the fundamentals of any transform from two to three dimensions is that the information in two dimensions is specified by integers but in three dimensions real numbers are required. If the visual processing systems of natural neural system are inference engines similar in nature to the sudoku system presented here then we would expect that the integer relationships from the initial facts are preserved as those facts are tranformed.